@(n) = Natural number factor collapsing algorithm

Below is the first 64 natural numbers visualized using the algorithm animation above. Click squares below to start animation for corresponding N value

Visualized below are the values of @(n) for the first natural numbers together with emergent prime gap distribution patterns

Hover over bars below to see corresponding integer - click to see corresponding gap set below (one visualization down)

Values appear in 3 horizontal bands according to the value of the prime gap in which they are located.

• Top: prime gaps = 6n + 2
• Bottom: prime gaps = 6n + 4
• Middle: prime gaps = 6n
• The middle band is subdivided into 2 further bands. Prime gaps in the top middle follow primes = 6n + 1 and prime gaps in the bottom middle follow primes = 6n - 1.

Each set visualizes all values from successive non-prime numbers that lay between successive pairs of prime numbers with equal prime gap. @(n) is equal to zero for all prime numbers which are not represented in these sets although could be thought of in this visualization as the negative space between each square. See corresponding colored values of @(n) in number line above. Values of @(n) are plotted here as semi transparent bars (height = value) so that average* values can be visualized.

* With this method of visualization, averages for the lower prime-gap sets will be distorted fractionally higher with greater values of n being processed.

Distribution of variation from average of the 4 number sets.

Notes (possibly all trivial) relating to 'Vortex math' (digital root emergent patterns)

Comparing the digital root of n to the digital root of the numerator (see animation above) of the rational output of the @(n) we see all values 1,2,4,5,7,8 get transformed to 3,6,9 and vice versa except those plotted on the graph by white and yellow outlines. Numbers outlined in white can be located by the following mod 81 periodic pattern

0 [3, 18 ,24, 30, 51, 57, 63, 78] 81
+3, [ +15, +6, +6, +21, +6, +6, +15, +6, +15, +6, +6, +21, +6, +6, +15, +6... ]

Some of the positions outlined yellow can be located with a +13, +14, +13, +14, +13, +14... sequence, but as yet I haven't looked carefully at this to see if all non-translated numbers can be accounted for by a finite set of periodic patterns.

The number of non translated numbers found in N tend towards 1 / 9N

@(n) algorithm as formula

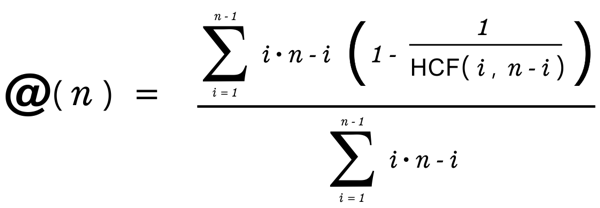
@(n) algorithm code

Example here is the JS used on this page to create the SVG visualisations

				
// gcd calcs greatest common divisor
			
var gcd = function( a, b ){
	
    if( ! b ){
        return a;
    }
    return gcd( b, a % b );
	
}



var nCollapse = function(n){
	
	var a = 0, b = 0, c = 0;
	
	for( var i = 1; i < n; i++ ){
	
		c = i * ( n - i );
		a += c * ( 1 - ( 1 / Math.pow( gcd( i, n - i ), 2 )));
		b += c;
		
	}
	return a / b;
	
}