Protofield (primitive)
Last updated March 2022
First thoughts
My interest in finding visual ways to represent infinity began in art school. I had heard people talk about how difficult it was for them to get-their-heads-around the idea of infinity and I even heard a friend say the idea scared him on some level. For whatever reason, for as long as I can remember, I felt more comfortable with the idea of infinity than the notion that anything could be assigned an arbitrary finite value. Looking back I wonder if I had or have a kind of hyperbolic dyslexia (That’s a joke). Something like hyperbolic geometry seemed a more natural way to articulate the world of inner experience, and even from a young age I felt the number line as it is conventionally known was, well, ugly. I didn’t like the fact it had a hole in it and that it could never fully be represented on a piece of paper. That was my intuitive sense anyway. Of course I am not arguing that the number line is not a very powerful and useful construct, but as a starting point to build language to describe our inner world of experience and consciousness it seemed like the wrong primitive. And as an artist, that was my lofty aspiration.

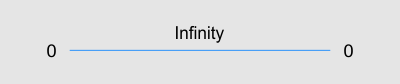
I actually remember the day I first sat down with pencil and paper and consciously started to think about ways to visually represent infinity. It was Easter day 1995. I started by drawing a line with a zero in the middle to represent the conventional number line with positive and negative infinity at either end.
Next I thought if I could go back before the big bang into absolute nothingness and tossed my pencil into that void, relative to that void my pencil would be infinite. Relative to nothing all things are infinite in a sense. n/0 = infinity. So I drew a line to represent a one dimensional line in the void with zero at either end and infinity in the middle. Keep in mind, here I was just thinking about finding very basic primitives from which to build something less abstract and ultimately an artistic expression.
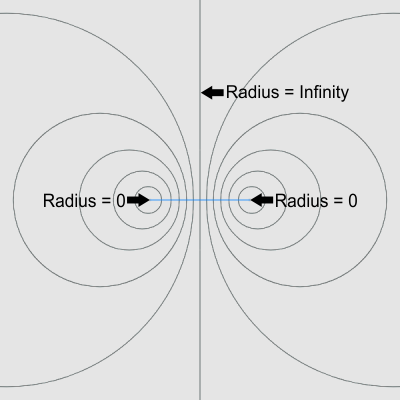
Next I thought about how best to represent change or difference along this line. I wanted a way to do this in a purely visual way so numbers were too symbolic and also numbers would bring us right back to some kind of arbitrary value system. Instead I thought of using circles because on some level they seemed to express infinity. So the radius of each circle can represent something that can change. Through the middle I drew a straight line like a y axis. This represented a circle with infinite radius, this was my upper limit. At the end of my infinity line were the two zeros. Here we have two points which could also be represented by circles with zero radius. It turns out that there is a natural geometric continuum of circles between these extremes that do not intersect. Intersections I felt would just add an additional level of complexity and at this point I was just looking for something pure and simple. I call this set of circles the protofield wave set.
This simple distribution pattern of circles is commonplace in geometry and is produced using Möbius Transformation. The structure also describes the distribution of electromagnetic fields.
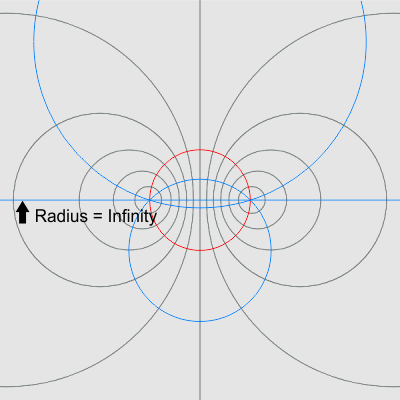
For reasons I will discuss later I call the red circle the origin circle. This circle is orthogonal (intersects at a right angle) to every circle in the protofield wave set. We can also draw any number of circles (examples in blue) that intersect the two zero points and they will also be orthogonal to the protofield wave set. Notice the original infinity line is a circle of infinite radius that belongs to this second orthogonal set of circles. I call this second set the orthogonal set.
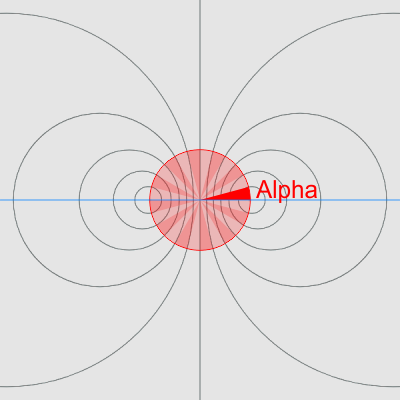
Typically, in most of my artistic constructions the protofield wave set intersects the origin circle at regular intervals around the origin circle. I call the angle that defines that interval Alpha. Generally when the wave interval is regular, as opposed to being exponential or random, the result when the protofield is rotated and combined (in the next step) is clearer and more crystalline.
The outputs seen in this project are constructed entirely from intersecting waves on a two dimensional surface not unlike ripples from multiple sources extending out on the surface of a pond. The surface in this method however, is just the area rendered on the screen so it is not a model of something actually physical. Unlike the ripples on a pond the waves here do not propagate concentrically from a source. Waves in this system propagate in a space that can be plotted by a simple Möbius transformation described below. This pattern in Hyperbolic space also describes a magnetic field around a dipole magnet.
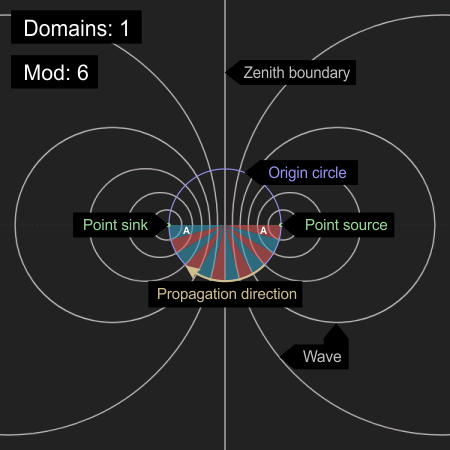
(Interactive) Fig.1.1 We have rotated the protofield within the origin circle 90 degrees and have given the origin circle free roam of the Y axis while constraining it by insisting it always passes through the two zero points. You can see how as the origin circle center shoots off to infinity the origin circle approaches becoming a straight line. As the origin circle passes through its zenith (straight line) we can get an intuitive sense of how the origin circle center can shoot off to infinity and return from negative infinity therefore seeing this progression as a continuum. However, as the origin circle passes its zenith boundary we can also see how the red and blue lines trade places so at one time the blue line is on the inside of the origin circle and at another it is on the outside. Like this we can also get an intuition on how this geometry rotates (twice) 720 degrees before returning to its original state. This is analogous to the certain types of spin in elementary physics.
Rotating and adding protfields to create quasi-cystals
Mod collapse harmonics
Related investigations
Layering quasi-crystals with mod = domains



