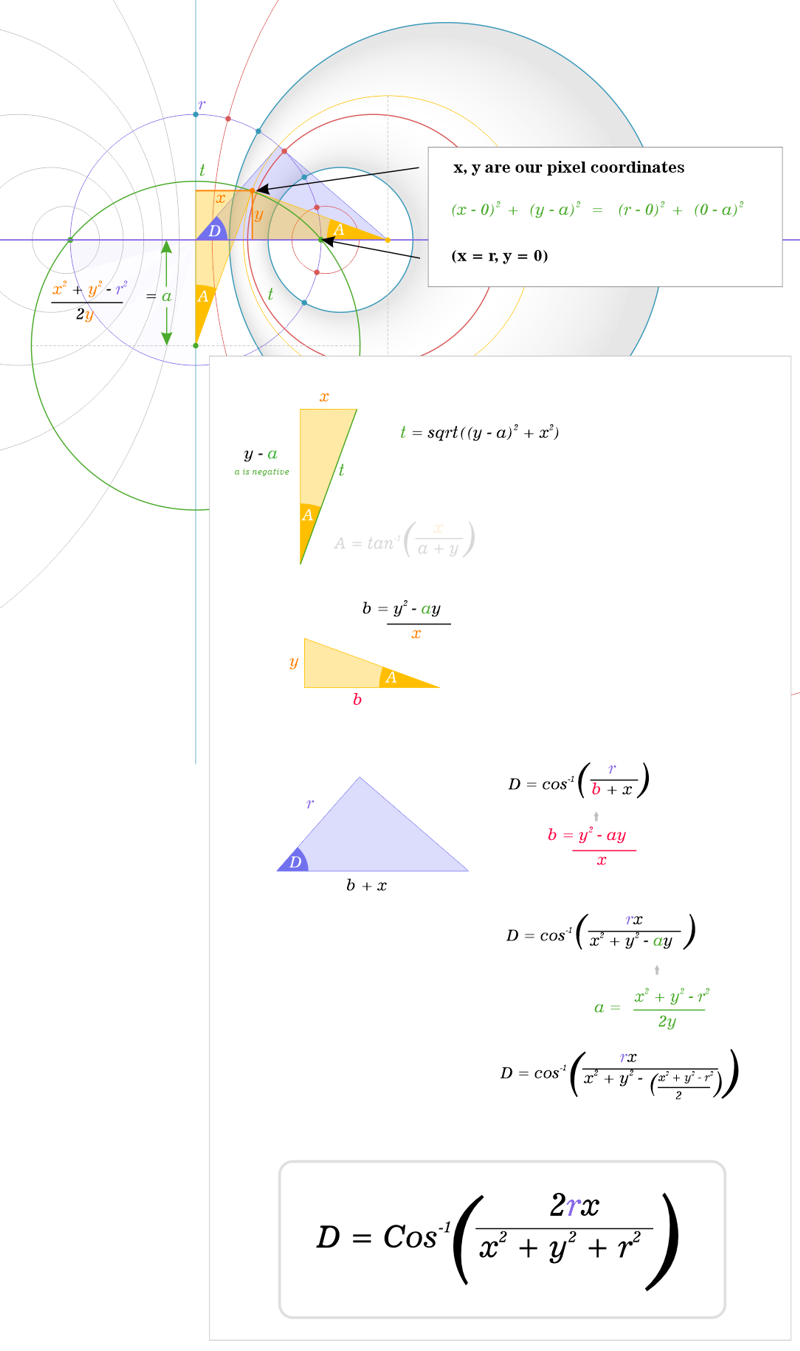
1. Construction method of protofield primitive

The wave configuration below I call a Protofiled. This primitive building block forms the basis of most of the generative art and animation I have produced over the last few years. It is fundamentally very simple, yet by rotating, combining and varying the frequencies of different protofield primitives we can produce a surprisingly rich set of visuals. I only discuss the fundamentals of the algorithm below and don't get into color or animation methods.

Hover over diagram above to change x, y input values


In this example wavelength is determined by the regular division of 'origin circle'

Frequencey: f  
X:
Y:
 a = (x2 + y2 - r2) / 2y
Wave orthoganal centerY:
 a
Wave orthoganal radius:
 √((y - a)2 + x2)
b = (y2 - ay) / x
Wave centerX:
 x + b
Wave center radius:
 √(b2 + y2)
D = Cos-1(r / (x + b))
Wave alpha:
 D
Wave:

2. Working drawings for above calculations

3. Rotating protofields to make a quasicrystal

Protofield primitive from above is simply rotated and wave values [-1...1] are summed for each rotation step. A single rotation step I call a Domain. In this example all domains have the same frequency. Looping through each domain is the source of the inefficiency in the algorithm. I wonder if there is a mathematical shortcut to summing each domain wave value for each pixel.

From above, wave value is calculated either by Sin(D * f) or Cos(D * f)



Rotation step:

Frequencey: 
Domains: 

Observations

When (Frequency is an integer and even) and (Domains is Even) and (Phase = Sine), waves cancel out completely